Regression Metrics:

MAE is more robust to data with outliers.

The lower value of MAE, MSE, and RMSE implies higher accuracy of a regression model. However, a higher value of R square is considered desirable.

R Squared & Adjusted R Squared are used for explaining how well the independent variables in the linear regression model explains the variability in the dependent variable.

For comparing the accuracy among different linear regression models, RMSE is a better choice than R Squared.

Use Mean Absolute Error when there are outliers and Mean Squared Error when you want to use as a loss function.

R2 (coefficient of determination)

R Square

% of variance in Y that is explained by X. It is defined as the square of correlation between Predicted and Actual values.
R2= SSEIndependent VarSSEIndependent Var + SSEErrors

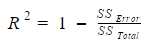
Adjusted R Square

Similar to R2. It penalizes for adding impurity (insignificant variables) to the model

Squared Error

MSE (Mean Squared Error)

Sum of squares / degree of freedom

RMSE (Root Mean Square Error)

It measures standard deviation of the residuals.

Model with the least RMSE is the best model
RMSE = sqrt (Sum of Squared Errors) / no of obs
= sqrt (mean ( (Actual - Predicted)2 ))

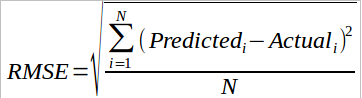
Absolute Error

MAE (Mean Absolute Error)

sum( |Error| ) / nError = Actual - Predicted |Error|=Absolute Error

MAPE (Mean Absolute Percentage Error)

{ absolute (average [ (Actual - Predicted) / Actual ])} should not exceed ~ 8% - 10%

Other Methods

RMSE is a better option as it is simple to calculate and differentiable. However, if your dataset has outliers then choose MAE over RMSE.

Loss Functions: objective is to minimize these

MAE : Mean Absolute Error (mean of the absolute errors)
MSE : Mean Squared Error (mean of the squared errors)
RMSE : Root Mean Squared Error (square root of the mean of squared errors)

☑️ Regression Metrics